Exploration-exploitation dilemma
[The original material for this note can be found in the introduction of the PhD thesis]
The mutation-selection process bears many similarities and analogies between other processes present in a variety of scientific fields outside evolutionary biology, displaying the same underlying mechanism and emerging properties, though with different names and aspirations. This note is an attempt to describe analogous processes and their emerging properties, such as to better appreciate and conceptualize its assumptions, its limits, and the respective role of the different components. Such attempts require to boil down the mutation-selection mechanism (see notes on Mutation-Selection models) into its core components, while at the same time rephrasing the description using lexicography outside of population genetics such as to open new perceiving angles.
At the bottom, mutation is a process creating diversity, changing and moving the current viable state to a novel and unknown position, fundamentally allowing exploration of the state space. On the other hand, selection is the criteria on which a new state is deemed a nonviable alteration, a disrupting innovation or repairing a rusted genome (see notes on non-adaptative beneficial mutations), and allows to determine which changes to exploit and which to filter out and discard based on its fitness. Fundamentally, mutation creates diversity and selection reduces this diversity by selecting the fittest mutants. Finally, drift arbitrates between the creation and reduction of the two processes, it dictates how much exploration of novelty is permitted, and conversely how much exploitation of only the fittest states is granted.
In this light, mutation and selection, exploration and exploitation, creation and reduction, are different names that ultimately encompass the inherently same process, efficiently sampling and optimizing whenever the state space is too large to be traversed in a finite amount of time or attempts:
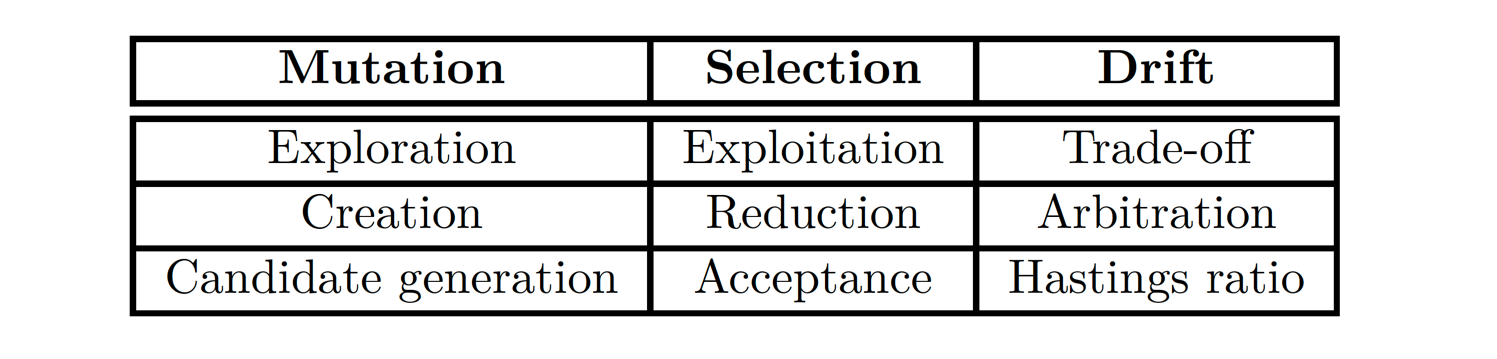
In the following, I seek to describe the mutation-selection process with two analogies: Metropolis-Hastings sampling and the exploration-exploitation dilemma.
Metropolis-Hastings sampling
Obtaining a sequence of random samples from a probability distribution can be difficult, especially when the number of dimensions is high. However, the Metropolis-Hastings procedure based on a Markov chain Monte Carlo can sample from any probability distribution, provided that we know how to compute the probability density, or even less restrictively any function proportional to the density. This stochastic procedure which is based on three steps bears many similarities with the mutation-selection process:
- Generate a stochastic candidate from the current state, analogous to mutation.
- Calculate the acceptance ratio as the ratio of the two densities, analogous to the selection coefficient of the mutated state.
- Stochastic acceptance or rejection based on the acceptance ratio, a process analogous to drift.
Inherently, the Metropolis-Hastings procedure is based on creating and subsequently reducing diversity, which allows to obtain a random sequence of samples from any distribution with a straightforward recipe, and is a critical tool in statistics and statistical physics.
The exploration-exploitation dilemma
Many mathematical, engineering and daily-life problems are not about sampling a state space, but rather about finding the optimal and best state given the criteria or a function to maximize. Naturally, we would prefer deterministic (strictly reproducible) rather than stochastic optimizing strategies to search for an optimal state. Unfortunately, whenever the state space is too large, often due to the curse of dimensionality, a greedy or heuristic search of an optimal state can perform atrociously. In high-dimensional space, stochastic optimization tools have been deemed very valuable, such as stochastic gradient descent or so-called evolutionary algorithms. Inherently, they are based on two processes, one is stochastically creating diversity and exploring the state space, while the other is filtering the explored states and thus reducing the diversity.
In the constrained case of a finite amount of time or attempts to find the best outcome overall, the problem is best described by the multi-armed bandit problem. The name comes from imagining a gambler at a row of slot machines (the one-armed bandits), where each slot machine provides a random reward from a probability distribution specific to that machine. The player has to decide which machines to play, how many times to play each machine and in which order to play them, and whether to continue with the current machine or try a different machine, such as to maximize the sum of rewards earned through a sequence of trials. The gambler faces a dilemma at each trial, either reducing his regret by exploiting the best arm, or gaining information through exploration of other arms. The best strategy to solve this dilemma can be mathematically derived in numerous cases, and encompasses mixing strategies with a defined ratio of exploration and exploitation. This problem is far from being only theoretical, and has been used to explain a multitude of phenomena, such as the movement of animals in novel landscapes, the most efficient resource allocation for a start-up company, the effects of age on knowledge acquisition in humans, and in the search of the most efficient treatment in clinical trials. Another application of the exploration-exploitation dilemma is AlphaGo, the first computational program mastering the board game Go at the professional 9-dan level in 2017, which outcompeted Ke Jie, the world first ranked player at the time. AlphaGo has often been publicized and hyped in various media outlets stating that this feat was possible due to machine learning, more specifically due to convolutional neural networks. However, it is more scarcely mentioned that the AlphaGo neural network is combined with an exploration-exploitation algorithm, or more specifically a Monte Carlo tree search. In practice, the convolutional neural network is used as a criterion to measure the advantage of a board configuration, but the different moves and paths probed and trimmed are done via an exploration-exploitation procedure.
Similarly as the Metropolis-Hastings procedure, the exploration-exploitation dilemma is based on creating and subsequently reducing diversity, which allows to find optimal states in a finite amount of time or attempts, and is a critical tool in machine learning, artificial intelligence, and decision-making.
Conclusion
Based on these analogies, I argue that evolutionary biologists, studying and leveraging the pervasive process of mutation and selection, can gain knowledge by recruiting insight and developments from other fields, much like there has been many crossovers between economics and evolution in the context of game theory. From a political standpoint, I also argue that scientific research endeavour is also an exploration-exploitation dilemma, which is arguably externally pressured to pursue exploitation, through funding of impactful research and a publish-or-perish systemic culture.
On a more artistic and lighter note, I imagined my PhD journey as a (random) walk exploring (phylogenetic) trees, (fitness) valleys, (adaptive) peaks, (Markov) chains, (drift) barriers and (mean) fields, as depicted in this watercolor made by my sister, Iris Latrille: